Tree-LSTM in DGL

Author: Zihao Ye, Qipeng Guo, Minjie Wang, Jake Zhao, Zheng Zhang

Warning

The tutorial aims at gaining insights into the paper, with code as a mean of explanation. The implementation thus is NOT optimized for running efficiency. For recommended implementation, please refer to the official examples.

import os

In this tutorial, you learn to use Tree-LSTM networks for sentiment analysis. The Tree-LSTM is a generalization of long short-term memory (LSTM) networks to tree-structured network topologies.

The Tree-LSTM structure was first introduced by Kai et. al in an ACL 2015 paper: Improved Semantic Representations From Tree-Structured Long Short-Term Memory Networks. The core idea is to introduce syntactic information for language tasks by extending the chain-structured LSTM to a tree-structured LSTM. The dependency tree and constituency tree techniques are leveraged to obtain a ‘’latent tree’’.

The challenge in training Tree-LSTMs is batching — a standard technique in machine learning to accelerate optimization. However, since trees generally have different shapes by nature, parallization is non-trivial. DGL offers an alternative. Pool all the trees into one single graph then induce the message passing over them, guided by the structure of each tree.

The task and the dataset

The steps here use the Stanford Sentiment Treebank in dgl.data. The dataset provides a fine-grained, tree-level sentiment annotation. There are five classes: Very negative, negative, neutral, positive, and very positive, which indicate the sentiment in the current subtree. Non-leaf nodes in a constituency tree do not contain words, so use a special PAD_WORD token to denote them. During training and inference their embeddings would be masked to all-zero.

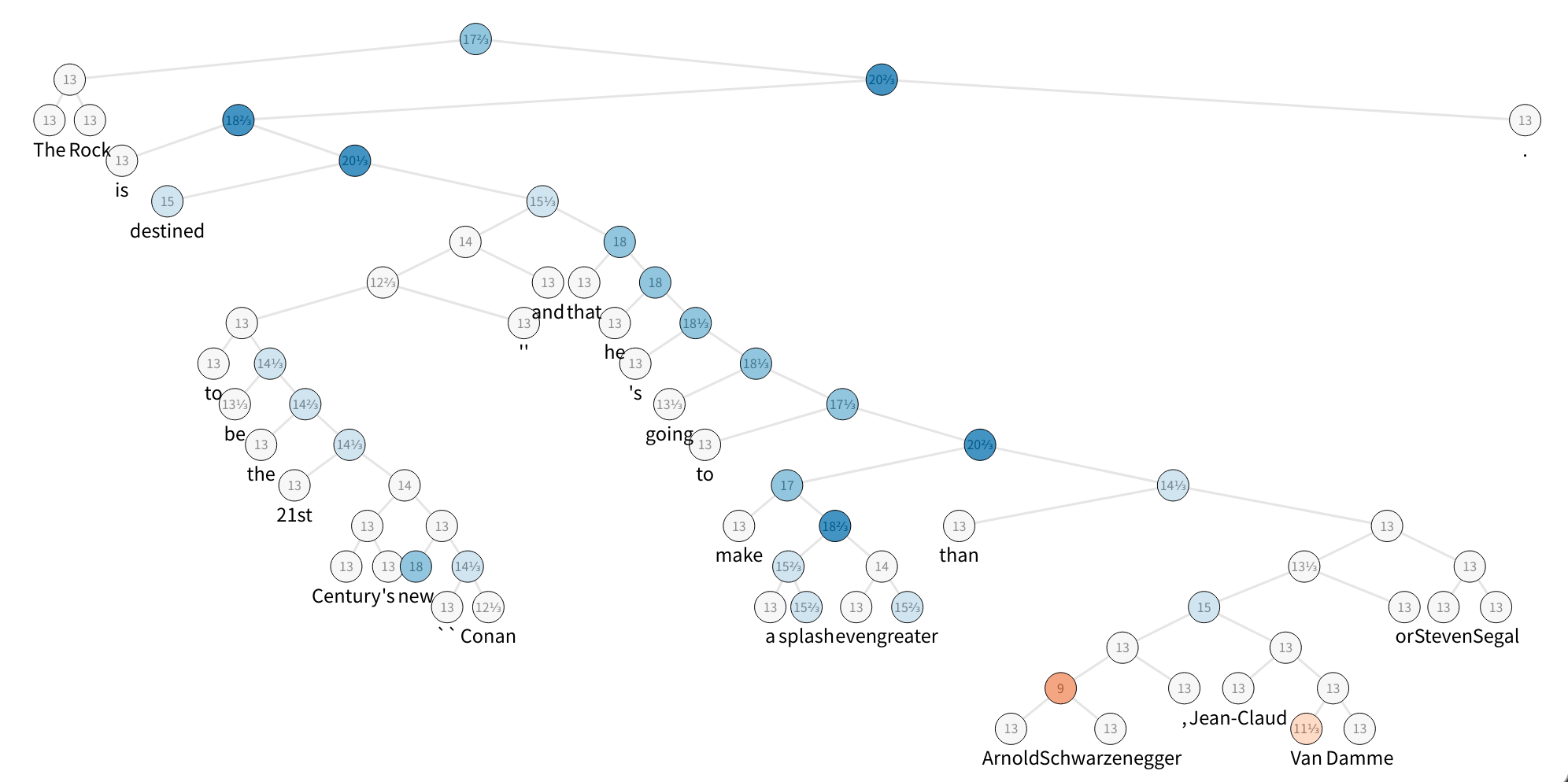
The figure displays one sample of the SST dataset, which is a constituency parse tree with their nodes labeled with sentiment. To speed up things, build a tiny set with five sentences and take a look at the first one.

from collections import namedtuple

os.environ["DGLBACKEND"] = "pytorch"
import dgl
from dgl.data.tree import SSTDataset


SSTBatch = namedtuple("SSTBatch", ["graph", "mask", "wordid", "label"])

# Each sample in the dataset is a constituency tree. The leaf nodes
# represent words. The word is an int value stored in the "x" field.
# The non-leaf nodes have a special word PAD_WORD. The sentiment
# label is stored in the "y" feature field.
trainset = SSTDataset(mode="tiny")  # the "tiny" set has only five trees
tiny_sst = [tr for tr in trainset]
num_vocabs = trainset.vocab_size
num_classes = trainset.num_classes

vocab = trainset.vocab  # vocabulary dict: key -> id
inv_vocab = {
    v: k for k, v in vocab.items()
}  # inverted vocabulary dict: id -> word

a_tree = tiny_sst[0]
for token in a_tree.ndata["x"].tolist():
    if token != trainset.PAD_WORD:
        print(inv_vocab[token], end=" ")
import matplotlib.pyplot as plt

the rock is destined to be the 21st century 's new `` conan '' and that he 's going to make a splash even greater than arnold schwarzenegger , jean-claud van damme or steven segal .

Step 1: Batching

Add all the trees to one graph, using the batch() API.

import networkx as nx

graph = dgl.batch(tiny_sst)


def plot_tree(g):
    # this plot requires pygraphviz package
    pos = nx.nx_agraph.graphviz_layout(g, prog="dot")
    nx.draw(
        g,
        pos,
        with_labels=False,
        node_size=10,
        node_color=[[0.5, 0.5, 0.5]],
        arrowsize=4,
    )
    plt.show()


plot_tree(graph.to_networkx())

You can read more about the definition of batch(), or skip ahead to the next step: .. note:

**Definition**: :func:`~dgl.batch` unions a list of :math:`B`
  :class:`~dgl.DGLGraph`\ s and returns a :class:`~dgl.DGLGraph` of batch
  size :math:`B`.

- The union includes all the nodes,
  edges, and their features. The order of nodes, edges, and features are
  preserved.

    - Given that you have :math:`V_i` nodes for graph
      :math:`\mathcal{G}_i`, the node ID :math:`j` in graph
      :math:`\mathcal{G}_i` correspond to node ID
      :math:`j + \sum_{k=1}^{i-1} V_k` in the batched graph.

    - Therefore, performing feature transformation and message passing on
      the batched graph is equivalent to doing those
      on all ``DGLGraph`` constituents in parallel.

- Duplicate references to the same graph are
  treated as deep copies; the nodes, edges, and features are duplicated,
  and mutation on one reference does not affect the other.
- The batched graph keeps track of the meta
  information of the constituents so it can be
  :func:`~dgl.batched_graph.unbatch`\ ed to list of ``DGLGraph``\ s.

Step 2: Tree-LSTM cell with message-passing APIs

Researchers have proposed two types of Tree-LSTMs: Child-Sum Tree-LSTMs, and \(N\)-ary Tree-LSTMs. In this tutorial you focus on applying Binary Tree-LSTM to binarized constituency trees. This application is also known as Constituency Tree-LSTM. Use PyTorch as a backend framework to set up the network.

In N-ary Tree-LSTM, each unit at node \(j\) maintains a hidden representation \(h_j\) and a memory cell \(c_j\). The unit \(j\) takes the input vector \(x_j\) and the hidden representations of the child units: \(h_{jl}, 1\leq l\leq N\) as input, then update its new hidden representation \(h_j\) and memory cell \(c_j\) by:

\[\begin{split}i_j & = & \sigma\left(W^{(i)}x_j + \sum_{l=1}^{N}U^{(i)}_l h_{jl} + b^{(i)}\right), & (1)\\ f_{jk} & = & \sigma\left(W^{(f)}x_j + \sum_{l=1}^{N}U_{kl}^{(f)} h_{jl} + b^{(f)} \right), & (2)\\ o_j & = & \sigma\left(W^{(o)}x_j + \sum_{l=1}^{N}U_{l}^{(o)} h_{jl} + b^{(o)} \right), & (3) \\ u_j & = & \textrm{tanh}\left(W^{(u)}x_j + \sum_{l=1}^{N} U_l^{(u)}h_{jl} + b^{(u)} \right), & (4)\\ c_j & = & i_j \odot u_j + \sum_{l=1}^{N} f_{jl} \odot c_{jl}, &(5) \\ h_j & = & o_j \cdot \textrm{tanh}(c_j), &(6) \\\end{split}\]

It can be decomposed into three phases: message_func, reduce_func and apply_node_func.

Note

apply_node_func is a new node UDF that has not been introduced before. In apply_node_func, a user specifies what to do with node features, without considering edge features and messages. In a Tree-LSTM case, apply_node_func is a must, since there exists (leaf) nodes with \(0\) incoming edges, which would not be updated with reduce_func.

import torch as th
import torch.nn as nn


class TreeLSTMCell(nn.Module):
    def __init__(self, x_size, h_size):
        super(TreeLSTMCell, self).__init__()
        self.W_iou = nn.Linear(x_size, 3 * h_size, bias=False)
        self.U_iou = nn.Linear(2 * h_size, 3 * h_size, bias=False)
        self.b_iou = nn.Parameter(th.zeros(1, 3 * h_size))
        self.U_f = nn.Linear(2 * h_size, 2 * h_size)

    def message_func(self, edges):
        return {"h": edges.src["h"], "c": edges.src["c"]}

    def reduce_func(self, nodes):
        # concatenate h_jl for equation (1), (2), (3), (4)
        h_cat = nodes.mailbox["h"].view(nodes.mailbox["h"].size(0), -1)
        # equation (2)
        f = th.sigmoid(self.U_f(h_cat)).view(*nodes.mailbox["h"].size())
        # second term of equation (5)
        c = th.sum(f * nodes.mailbox["c"], 1)
        return {"iou": self.U_iou(h_cat), "c": c}

    def apply_node_func(self, nodes):
        # equation (1), (3), (4)
        iou = nodes.data["iou"] + self.b_iou
        i, o, u = th.chunk(iou, 3, 1)
        i, o, u = th.sigmoid(i), th.sigmoid(o), th.tanh(u)
        # equation (5)
        c = i * u + nodes.data["c"]
        # equation (6)
        h = o * th.tanh(c)
        return {"h": h, "c": c}

Step 3: Define traversal

After you define the message-passing functions, induce the right order to trigger them. This is a significant departure from models such as GCN, where all nodes are pulling messages from upstream ones simultaneously.

In the case of Tree-LSTM, messages start from leaves of the tree, and propagate/processed upwards until they reach the roots. A visualization is as follows:

DGL defines a generator to perform the topological sort, each item is a tensor recording the nodes from bottom level to the roots. One can appreciate the degree of parallelism by inspecting the difference of the followings:

# to heterogenous graph
trv_a_tree = dgl.graph(a_tree.edges())
print("Traversing one tree:")
print(dgl.topological_nodes_generator(trv_a_tree))

# to heterogenous graph
trv_graph = dgl.graph(graph.edges())
print("Traversing many trees at the same time:")
print(dgl.topological_nodes_generator(trv_graph))

Traversing one tree:
(tensor([ 2,  3,  6,  8, 13, 15, 17, 19, 22, 23, 25, 27, 28, 29, 30, 32, 34, 36,
        38, 40, 43, 46, 47, 49, 50, 52, 58, 59, 60, 62, 64, 65, 66, 68, 69, 70]), tensor([ 1, 21, 26, 45, 48, 57, 63, 67]), tensor([24, 44, 56, 61]), tensor([20, 42, 55]), tensor([18, 54]), tensor([16, 53]), tensor([14, 51]), tensor([12, 41]), tensor([11, 39]), tensor([10, 37]), tensor([35]), tensor([33]), tensor([31]), tensor([9]), tensor([7]), tensor([5]), tensor([4]), tensor([0]))
Traversing many trees at the same time:
(tensor([  2,   3,   6,   8,  13,  15,  17,  19,  22,  23,  25,  27,  28,  29,
         30,  32,  34,  36,  38,  40,  43,  46,  47,  49,  50,  52,  58,  59,
         60,  62,  64,  65,  66,  68,  69,  70,  74,  76,  78,  79,  82,  83,
         85,  88,  90,  92,  93,  95,  96, 100, 102, 103, 105, 109, 110, 112,
        113, 117, 118, 119, 121, 125, 127, 129, 130, 132, 133, 135, 138, 140,
        141, 142, 143, 150, 152, 153, 155, 158, 159, 161, 162, 164, 168, 170,
        171, 174, 175, 178, 179, 182, 184, 185, 187, 189, 190, 191, 192, 195,
        197, 198, 200, 202, 205, 208, 210, 212, 213, 214, 216, 218, 219, 220,
        223, 225, 227, 229, 230, 232, 235, 237, 240, 242, 244, 246, 248, 249,
        251, 253, 255, 256, 257, 259, 262, 263, 267, 269, 270, 271, 272]), tensor([  1,  21,  26,  45,  48,  57,  63,  67,  77,  81,  91,  94, 101, 108,
        111, 116, 128, 131, 139, 151, 157, 160, 169, 173, 177, 183, 188, 196,
        211, 217, 228, 247, 254, 261, 268]), tensor([ 24,  44,  56,  61,  75,  89,  99, 107, 115, 126, 137, 149, 156, 167,
        181, 186, 194, 209, 215, 226, 245, 252, 266]), tensor([ 20,  42,  55,  73,  87, 124, 136, 154, 180, 207, 224, 243, 250, 265]), tensor([ 18,  54,  86, 123, 134, 148, 176, 206, 222, 241, 264]), tensor([ 16,  53,  84, 122, 172, 204, 239, 260]), tensor([ 14,  51,  80, 120, 166, 203, 238, 258]), tensor([ 12,  41,  72, 114, 165, 201, 236]), tensor([ 11,  39, 106, 163, 199, 234]), tensor([ 10,  37, 104, 147, 193, 233]), tensor([ 35,  98, 146, 231]), tensor([ 33,  97, 145, 221]), tensor([ 31,  71, 144]), tensor([9]), tensor([7]), tensor([5]), tensor([4]), tensor([0]))

Call prop_nodes() to trigger the message passing:

import dgl.function as fn
import torch as th

trv_graph.ndata["a"] = th.ones(graph.num_nodes(), 1)
traversal_order = dgl.topological_nodes_generator(trv_graph)
trv_graph.prop_nodes(
    traversal_order,
    message_func=fn.copy_u("a", "a"),
    reduce_func=fn.sum("a", "a"),
)

# the following is a syntax sugar that does the same
# dgl.prop_nodes_topo(graph)

Note

Before you call prop_nodes(), specify a message_func and reduce_func in advance. In the example, you can see built-in copy-from-source and sum functions as message functions, and a reduce function for demonstration.

Putting it together

Here is the complete code that specifies the Tree-LSTM class.

class TreeLSTM(nn.Module):
    def __init__(
        self,
        num_vocabs,
        x_size,
        h_size,
        num_classes,
        dropout,
        pretrained_emb=None,
    ):
        super(TreeLSTM, self).__init__()
        self.x_size = x_size
        self.embedding = nn.Embedding(num_vocabs, x_size)
        if pretrained_emb is not None:
            print("Using glove")
            self.embedding.weight.data.copy_(pretrained_emb)
            self.embedding.weight.requires_grad = True
        self.dropout = nn.Dropout(dropout)
        self.linear = nn.Linear(h_size, num_classes)
        self.cell = TreeLSTMCell(x_size, h_size)

    def forward(self, batch, h, c):
        """Compute tree-lstm prediction given a batch.

        Parameters
        ----------
        batch : dgl.data.SSTBatch
            The data batch.
        h : Tensor
            Initial hidden state.
        c : Tensor
            Initial cell state.

        Returns
        -------
        logits : Tensor
            The prediction of each node.
        """
        g = batch.graph
        # to heterogenous graph
        g = dgl.graph(g.edges())
        # feed embedding
        embeds = self.embedding(batch.wordid * batch.mask)
        g.ndata["iou"] = self.cell.W_iou(
            self.dropout(embeds)
        ) * batch.mask.float().unsqueeze(-1)
        g.ndata["h"] = h
        g.ndata["c"] = c
        # propagate
        dgl.prop_nodes_topo(
            g,
            message_func=self.cell.message_func,
            reduce_func=self.cell.reduce_func,
            apply_node_func=self.cell.apply_node_func,
        )
        # compute logits
        h = self.dropout(g.ndata.pop("h"))
        logits = self.linear(h)
        return logits


import torch.nn.functional as F

Main Loop

Finally, you could write a training paradigm in PyTorch.

from torch.utils.data import DataLoader

device = th.device("cpu")
# hyper parameters
x_size = 256
h_size = 256
dropout = 0.5
lr = 0.05
weight_decay = 1e-4
epochs = 10

# create the model
model = TreeLSTM(
    trainset.vocab_size, x_size, h_size, trainset.num_classes, dropout
)
print(model)

# create the optimizer
optimizer = th.optim.Adagrad(
    model.parameters(), lr=lr, weight_decay=weight_decay
)


def batcher(dev):
    def batcher_dev(batch):
        batch_trees = dgl.batch(batch)
        return SSTBatch(
            graph=batch_trees,
            mask=batch_trees.ndata["mask"].to(device),
            wordid=batch_trees.ndata["x"].to(device),
            label=batch_trees.ndata["y"].to(device),
        )

    return batcher_dev


train_loader = DataLoader(
    dataset=tiny_sst,
    batch_size=5,
    collate_fn=batcher(device),
    shuffle=False,
    num_workers=0,
)

# training loop
for epoch in range(epochs):
    for step, batch in enumerate(train_loader):
        g = batch.graph
        n = g.num_nodes()
        h = th.zeros((n, h_size))
        c = th.zeros((n, h_size))
        logits = model(batch, h, c)
        logp = F.log_softmax(logits, 1)
        loss = F.nll_loss(logp, batch.label, reduction="sum")
        optimizer.zero_grad()
        loss.backward()
        optimizer.step()
        pred = th.argmax(logits, 1)
        acc = float(th.sum(th.eq(batch.label, pred))) / len(batch.label)
        print(
            "Epoch {:05d} | Step {:05d} | Loss {:.4f} | Acc {:.4f} |".format(
                epoch, step, loss.item(), acc
            )
        )

TreeLSTM(
  (embedding): Embedding(19536, 256)
  (dropout): Dropout(p=0.5, inplace=False)
  (linear): Linear(in_features=256, out_features=5, bias=True)
  (cell): TreeLSTMCell(
    (W_iou): Linear(in_features=256, out_features=768, bias=False)
    (U_iou): Linear(in_features=512, out_features=768, bias=False)
    (U_f): Linear(in_features=512, out_features=512, bias=True)
  )
)
/home/ubuntu/prod-doc/readthedocs.org/user_builds/dgl/checkouts/2.2.x/python/dgl/core.py:82: DGLWarning: The input graph for the user-defined edge function does not contain valid edges
  dgl_warning(
Epoch 00000 | Step 00000 | Loss 425.6214 | Acc 0.3297 |
Epoch 00001 | Step 00000 | Loss 276.5078 | Acc 0.7363 |
Epoch 00002 | Step 00000 | Loss 1219.3381 | Acc 0.2674 |
Epoch 00003 | Step 00000 | Loss 324.3909 | Acc 0.5604 |
Epoch 00004 | Step 00000 | Loss 169.2826 | Acc 0.8242 |
Epoch 00005 | Step 00000 | Loss 461.1243 | Acc 0.6447 |
Epoch 00006 | Step 00000 | Loss 242.7960 | Acc 0.8425 |
Epoch 00007 | Step 00000 | Loss 188.4147 | Acc 0.7875 |
Epoch 00008 | Step 00000 | Loss 121.0420 | Acc 0.8535 |
Epoch 00009 | Step 00000 | Loss 95.1390 | Acc 0.9048 |

To train the model on a full dataset with different settings (such as CPU or GPU), refer to the PyTorch example. There is also an implementation of the Child-Sum Tree-LSTM.