Understand Graph Attention Network

Authors: Hao Zhang, Mufei Li, Minjie Wang Zheng Zhang

Warning

The tutorial aims at gaining insights into the paper, with code as a mean of explanation. The implementation thus is NOT optimized for running efficiency. For recommended implementation, please refer to the official examples.

In this tutorial, you learn about a graph attention network (GAT) and how it can be implemented in PyTorch. You can also learn to visualize and understand what the attention mechanism has learned.

The research described in the paper Graph Convolutional Network (GCN), indicates that combining local graph structure and node-level features yields good performance on node classification tasks. However, the way GCN aggregates is structure-dependent, which can hurt its generalizability.

One workaround is to simply average over all neighbor node features as described in the research paper GraphSAGE. However, Graph Attention Network proposes a different type of aggregation. GAT uses weighting neighbor features with feature dependent and structure-free normalization, in the style of attention.

Introducing attention to GCN

The key difference between GAT and GCN is how the information from the one-hop neighborhood is aggregated.

For GCN, a graph convolution operation produces the normalized sum of the node features of neighbors.

\[h_i^{(l+1)}=\sigma\left(\sum_{j\in \mathcal{N}(i)} {\frac{1}{c_{ij}} W^{(l)}h^{(l)}_j}\right)\]

where \(\mathcal{N}(i)\) is the set of its one-hop neighbors (to include \(v_i\) in the set, simply add a self-loop to each node), \(c_{ij}=\sqrt{|\mathcal{N}(i)|}\sqrt{|\mathcal{N}(j)|}\) is a normalization constant based on graph structure, \(\sigma\) is an activation function (GCN uses ReLU), and \(W^{(l)}\) is a shared weight matrix for node-wise feature transformation. Another model proposed in GraphSAGE employs the same update rule except that they set \(c_{ij}=|\mathcal{N}(i)|\).

GAT introduces the attention mechanism as a substitute for the statically normalized convolution operation. Below are the equations to compute the node embedding \(h_i^{(l+1)}\) of layer \(l+1\) from the embeddings of layer \(l\).

\[\begin{split}\begin{align} z_i^{(l)}&=W^{(l)}h_i^{(l)},&(1) \\ e_{ij}^{(l)}&=\text{LeakyReLU}(\vec a^{(l)^T}(z_i^{(l)}||z_j^{(l)})),&(2)\\ \alpha_{ij}^{(l)}&=\frac{\exp(e_{ij}^{(l)})}{\sum_{k\in \mathcal{N}(i)}^{}\exp(e_{ik}^{(l)})},&(3)\\ h_i^{(l+1)}&=\sigma\left(\sum_{j\in \mathcal{N}(i)} {\alpha^{(l)}_{ij} z^{(l)}_j }\right),&(4) \end{align}\end{split}\]

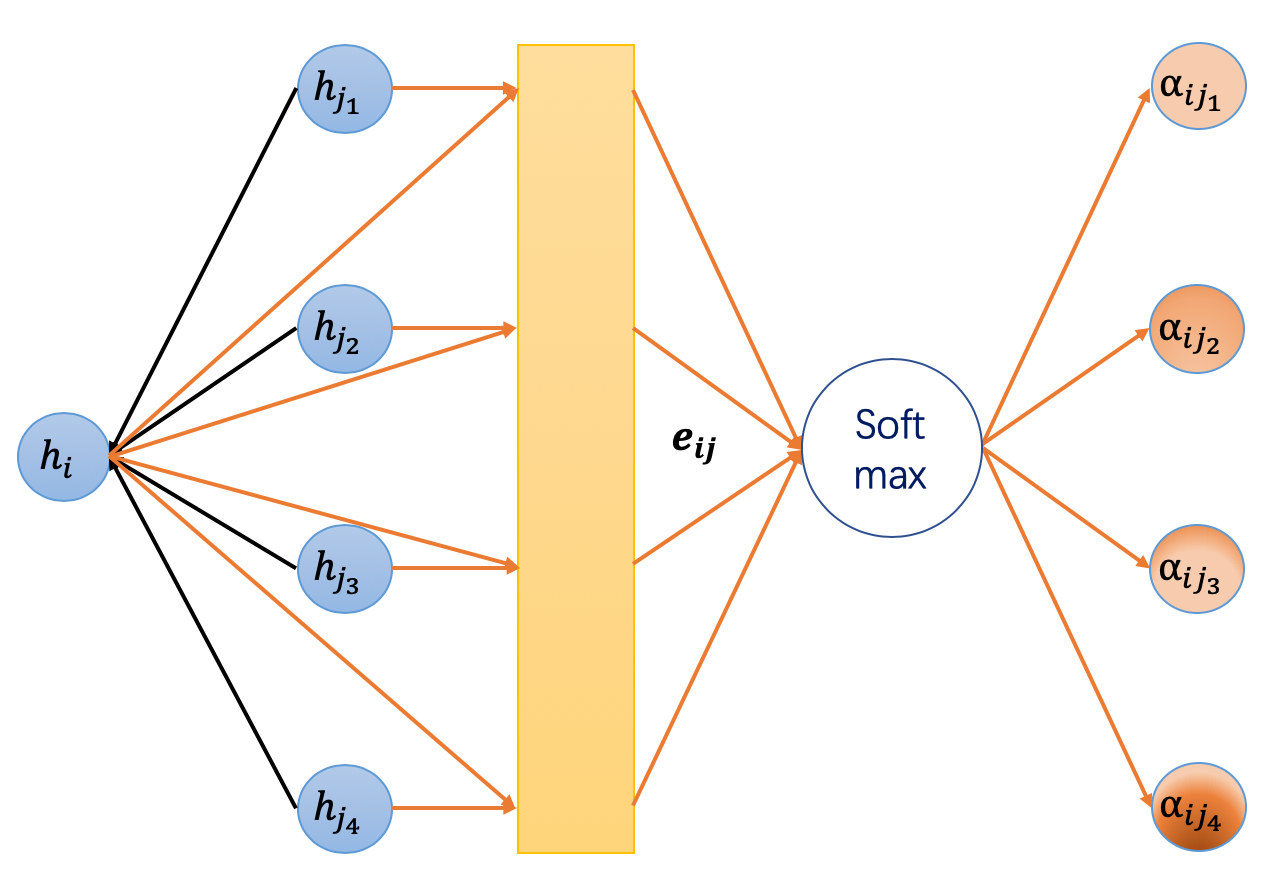
Explanations:

• Equation (1) is a linear transformation of the lower layer embedding \(h_i^{(l)}\) and \(W^{(l)}\) is its learnable weight matrix.

• Equation (2) computes a pair-wise un-normalized attention score between two neighbors. Here, it first concatenates the \(z\) embeddings of the two nodes, where \(||\) denotes concatenation, then takes a dot product of it and a learnable weight vector \(\vec a^{(l)}\), and applies a LeakyReLU in the end. This form of attention is usually called additive attention, contrast with the dot-product attention in the Transformer model.

• Equation (3) applies a softmax to normalize the attention scores on each node’s incoming edges.

• Equation (4) is similar to GCN. The embeddings from neighbors are aggregated together, scaled by the attention scores.

There are other details from the paper, such as dropout and skip connections. For the purpose of simplicity, those details are left out of this tutorial. To see more details, download the full example. In its essence, GAT is just a different aggregation function with attention over features of neighbors, instead of a simple mean aggregation.

GAT in DGL

DGL provides an off-the-shelf implementation of the GAT layer under the dgl.nn.<backend> subpackage. Simply import the GATConv as the follows.

import os

os.environ["DGLBACKEND"] = "pytorch"

Readers can skip the following step-by-step explanation of the implementation and jump to the Put everything together for training and visualization results.

To begin, you can get an overall impression about how a GATLayer module is implemented in DGL. In this section, the four equations above are broken down one at a time.

Note

This is showing how to implement a GAT from scratch. DGL provides a more efficient builtin GAT layer module.

import torch
import torch.nn as nn
import torch.nn.functional as F
from dgl.nn.pytorch import GATConv


class GATLayer(nn.Module):
    def __init__(self, g, in_dim, out_dim):
        super(GATLayer, self).__init__()
        self.g = g
        # equation (1)
        self.fc = nn.Linear(in_dim, out_dim, bias=False)
        # equation (2)
        self.attn_fc = nn.Linear(2 * out_dim, 1, bias=False)
        self.reset_parameters()

    def reset_parameters(self):
        """Reinitialize learnable parameters."""
        gain = nn.init.calculate_gain("relu")
        nn.init.xavier_normal_(self.fc.weight, gain=gain)
        nn.init.xavier_normal_(self.attn_fc.weight, gain=gain)

    def edge_attention(self, edges):
        # edge UDF for equation (2)
        z2 = torch.cat([edges.src["z"], edges.dst["z"]], dim=1)
        a = self.attn_fc(z2)
        return {"e": F.leaky_relu(a)}

    def message_func(self, edges):
        # message UDF for equation (3) & (4)
        return {"z": edges.src["z"], "e": edges.data["e"]}

    def reduce_func(self, nodes):
        # reduce UDF for equation (3) & (4)
        # equation (3)
        alpha = F.softmax(nodes.mailbox["e"], dim=1)
        # equation (4)
        h = torch.sum(alpha * nodes.mailbox["z"], dim=1)
        return {"h": h}

    def forward(self, h):
        # equation (1)
        z = self.fc(h)
        self.g.ndata["z"] = z
        # equation (2)
        self.g.apply_edges(self.edge_attention)
        # equation (3) & (4)
        self.g.update_all(self.message_func, self.reduce_func)
        return self.g.ndata.pop("h")

Equation (1)

\[z_i^{(l)}=W^{(l)}h_i^{(l)},(1)\]

The first one shows linear transformation. It’s common and can be easily implemented in Pytorch using torch.nn.Linear.

Equation (2)

\[e_{ij}^{(l)}=\text{LeakyReLU}(\vec a^{(l)^T}(z_i^{(l)}|z_j^{(l)})),(2)\]

The un-normalized attention score \(e_{ij}\) is calculated using the embeddings of adjacent nodes \(i\) and \(j\). This suggests that the attention scores can be viewed as edge data, which can be calculated by the apply_edges API. The argument to the apply_edges is an Edge UDF, which is defined as below:

def edge_attention(self, edges):
    # edge UDF for equation (2)
    z2 = torch.cat([edges.src["z"], edges.dst["z"]], dim=1)
    a = self.attn_fc(z2)
    return {"e": F.leaky_relu(a)}

Here, the dot product with the learnable weight vector \(\vec{a^{(l)}}\) is implemented again using PyTorch’s linear transformation attn_fc. Note that apply_edges will batch all the edge data in one tensor, so the cat, attn_fc here are applied on all the edges in parallel.

Equation (3) & (4)

\[\begin{split}\begin{align} \alpha_{ij}^{(l)}&=\frac{\exp(e_{ij}^{(l)})}{\sum_{k\in \mathcal{N}(i)}^{}\exp(e_{ik}^{(l)})},&(3)\\ h_i^{(l+1)}&=\sigma\left(\sum_{j\in \mathcal{N}(i)} {\alpha^{(l)}_{ij} z^{(l)}_j }\right),&(4) \end{align}\end{split}\]

Similar to GCN, update_all API is used to trigger message passing on all the nodes. The message function sends out two tensors: the transformed z embedding of the source node and the un-normalized attention score e on each edge. The reduce function then performs two tasks:

• Normalize the attention scores using softmax (equation (3)).

• Aggregate neighbor embeddings weighted by the attention scores (equation(4)).

Both tasks first fetch data from the mailbox and then manipulate it on the second dimension (dim=1), on which the messages are batched.

def reduce_func(self, nodes):
    # reduce UDF for equation (3) & (4)
    # equation (3)
    alpha = F.softmax(nodes.mailbox["e"], dim=1)
    # equation (4)
    h = torch.sum(alpha * nodes.mailbox["z"], dim=1)
    return {"h": h}

Multi-head attention

Analogous to multiple channels in ConvNet, GAT introduces multi-head attention to enrich the model capacity and to stabilize the learning process. Each attention head has its own parameters and their outputs can be merged in two ways:

\[\text{concatenation}: h^{(l+1)}_{i} =||_{k=1}^{K}\sigma\left(\sum_{j\in \mathcal{N}(i)}\alpha_{ij}^{k}W^{k}h^{(l)}_{j}\right)\]

or

\[\text{average}: h_{i}^{(l+1)}=\sigma\left(\frac{1}{K}\sum_{k=1}^{K}\sum_{j\in\mathcal{N}(i)}\alpha_{ij}^{k}W^{k}h^{(l)}_{j}\right)\]

where \(K\) is the number of heads. You can use concatenation for intermediary layers and average for the final layer.

Use the above defined single-head GATLayer as the building block for the MultiHeadGATLayer below:

class MultiHeadGATLayer(nn.Module):
    def __init__(self, g, in_dim, out_dim, num_heads, merge="cat"):
        super(MultiHeadGATLayer, self).__init__()
        self.heads = nn.ModuleList()
        for i in range(num_heads):
            self.heads.append(GATLayer(g, in_dim, out_dim))
        self.merge = merge

    def forward(self, h):
        head_outs = [attn_head(h) for attn_head in self.heads]
        if self.merge == "cat":
            # concat on the output feature dimension (dim=1)
            return torch.cat(head_outs, dim=1)
        else:
            # merge using average
            return torch.mean(torch.stack(head_outs))

Put everything together

Now, you can define a two-layer GAT model.

class GAT(nn.Module):
    def __init__(self, g, in_dim, hidden_dim, out_dim, num_heads):
        super(GAT, self).__init__()
        self.layer1 = MultiHeadGATLayer(g, in_dim, hidden_dim, num_heads)
        # Be aware that the input dimension is hidden_dim*num_heads since
        # multiple head outputs are concatenated together. Also, only
        # one attention head in the output layer.
        self.layer2 = MultiHeadGATLayer(g, hidden_dim * num_heads, out_dim, 1)

    def forward(self, h):
        h = self.layer1(h)
        h = F.elu(h)
        h = self.layer2(h)
        return h


import networkx as nx

We then load the Cora dataset using DGL’s built-in data module.

from dgl import DGLGraph
from dgl.data import citation_graph as citegrh


def load_cora_data():
    data = citegrh.load_cora()
    g = data[0]
    mask = torch.BoolTensor(g.ndata["train_mask"])
    return g, g.ndata["feat"], g.ndata["label"], mask

The training loop is exactly the same as in the GCN tutorial.

import time

import numpy as np

g, features, labels, mask = load_cora_data()

# create the model, 2 heads, each head has hidden size 8
net = GAT(g, in_dim=features.size()[1], hidden_dim=8, out_dim=7, num_heads=2)

# create optimizer
optimizer = torch.optim.Adam(net.parameters(), lr=1e-3)

# main loop
dur = []
for epoch in range(30):
    if epoch >= 3:
        t0 = time.time()

    logits = net(features)
    logp = F.log_softmax(logits, 1)
    loss = F.nll_loss(logp[mask], labels[mask])

    optimizer.zero_grad()
    loss.backward()
    optimizer.step()

    if epoch >= 3:
        dur.append(time.time() - t0)

    print(
        "Epoch {:05d} | Loss {:.4f} | Time(s) {:.4f}".format(
            epoch, loss.item(), np.mean(dur)
        )
    )

  NumNodes: 2708
  NumEdges: 10556
  NumFeats: 1433
  NumClasses: 7
  NumTrainingSamples: 140
  NumValidationSamples: 500
  NumTestSamples: 1000
Done loading data from cached files.
/home/ubuntu/prod-doc/readthedocs.org/user_builds/dgl/envs/2.2.x/lib/python3.8/site-packages/numpy/core/fromnumeric.py:3464: RuntimeWarning: Mean of empty slice.
  return _methods._mean(a, axis=axis, dtype=dtype,
/home/ubuntu/prod-doc/readthedocs.org/user_builds/dgl/envs/2.2.x/lib/python3.8/site-packages/numpy/core/_methods.py:192: RuntimeWarning: invalid value encountered in scalar divide
  ret = ret.dtype.type(ret / rcount)
Epoch 00000 | Loss 1.9480 | Time(s) nan
Epoch 00001 | Loss 1.9460 | Time(s) nan
Epoch 00002 | Loss 1.9439 | Time(s) nan
Epoch 00003 | Loss 1.9418 | Time(s) 0.1486
Epoch 00004 | Loss 1.9397 | Time(s) 0.1484
Epoch 00005 | Loss 1.9376 | Time(s) 0.1482
Epoch 00006 | Loss 1.9356 | Time(s) 0.1484
Epoch 00007 | Loss 1.9335 | Time(s) 0.1481
Epoch 00008 | Loss 1.9314 | Time(s) 0.1480
Epoch 00009 | Loss 1.9293 | Time(s) 0.1480
Epoch 00010 | Loss 1.9272 | Time(s) 0.1483
Epoch 00011 | Loss 1.9251 | Time(s) 0.1481
Epoch 00012 | Loss 1.9230 | Time(s) 0.1482
Epoch 00013 | Loss 1.9209 | Time(s) 0.1483
Epoch 00014 | Loss 1.9188 | Time(s) 0.1484
Epoch 00015 | Loss 1.9166 | Time(s) 0.1486
Epoch 00016 | Loss 1.9145 | Time(s) 0.1485
Epoch 00017 | Loss 1.9123 | Time(s) 0.1484
Epoch 00018 | Loss 1.9102 | Time(s) 0.1484
Epoch 00019 | Loss 1.9080 | Time(s) 0.1484
Epoch 00020 | Loss 1.9058 | Time(s) 0.1485
Epoch 00021 | Loss 1.9036 | Time(s) 0.1485
Epoch 00022 | Loss 1.9014 | Time(s) 0.1486
Epoch 00023 | Loss 1.8992 | Time(s) 0.1486
Epoch 00024 | Loss 1.8970 | Time(s) 0.1486
Epoch 00025 | Loss 1.8948 | Time(s) 0.1486
Epoch 00026 | Loss 1.8925 | Time(s) 0.1485
Epoch 00027 | Loss 1.8903 | Time(s) 0.1485
Epoch 00028 | Loss 1.8880 | Time(s) 0.1485
Epoch 00029 | Loss 1.8857 | Time(s) 0.1486

Visualizing and understanding attention learned

Cora

The following table summarizes the model performance on Cora that is reported in the GAT paper and obtained with DGL implementations.

Model	Accuracy
GCN (paper)	\(81.4\pm 0.5%\)
GCN (dgl)	\(82.05\pm 0.33%\)
GAT (paper)	\(83.0\pm 0.7%\)
GAT (dgl)	\(83.69\pm 0.529%\)

What kind of attention distribution has our model learned?

Because the attention weight \(a_{ij}\) is associated with edges, you can visualize it by coloring edges. Below you can pick a subgraph of Cora and plot the attention weights of the last GATLayer. The nodes are colored according to their labels, whereas the edges are colored according to the magnitude of the attention weights, which can be referred with the colorbar on the right.

You can see that the model seems to learn different attention weights. To understand the distribution more thoroughly, measure the entropy) of the attention distribution. For any node \(i\), \(\{\alpha_{ij}\}_{j\in\mathcal{N}(i)}\) forms a discrete probability distribution over all its neighbors with the entropy given by

\[H({\alpha_{ij}}_{j\in\mathcal{N}(i)})=-\sum_{j\in\mathcal{N}(i)} \alpha_{ij}\log\alpha_{ij}\]

A low entropy means a high degree of concentration, and vice versa. An entropy of 0 means all attention is on one source node. The uniform distribution has the highest entropy of \(\log(\mathcal{N}(i))\). Ideally, you want to see the model learns a distribution of lower entropy (i.e, one or two neighbors are much more important than the others).

Note that since nodes can have different degrees, the maximum entropy will also be different. Therefore, you plot the aggregated histogram of entropy values of all nodes in the entire graph. Below are the attention histogram of learned by each attention head.

As a reference, here is the histogram if all the nodes have uniform attention weight distribution.

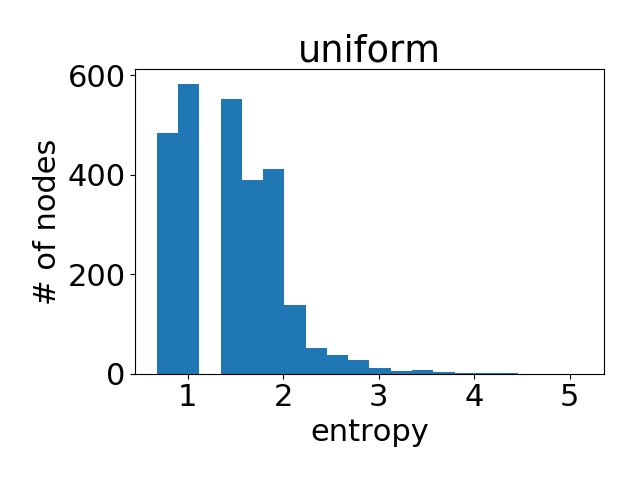
One can see that the attention values learned is quite similar to uniform distribution (i.e, all neighbors are equally important). This partially explains why the performance of GAT is close to that of GCN on Cora (according to author’s reported result, the accuracy difference averaged over 100 runs is less than 2 percent). Attention does not matter since it does not differentiate much.

Does that mean the attention mechanism is not useful? No! A different dataset exhibits an entirely different pattern, as you can see next.

Protein-protein interaction (PPI) networks

The PPI dataset used here consists of \(24\) graphs corresponding to different human tissues. Nodes can have up to \(121\) kinds of labels, so the label of node is represented as a binary tensor of size \(121\). The task is to predict node label.

Use \(20\) graphs for training, \(2\) for validation and \(2\) for test. The average number of nodes per graph is \(2372\). Each node has \(50\) features that are composed of positional gene sets, motif gene sets, and immunological signatures. Critically, test graphs remain completely unobserved during training, a setting called “inductive learning”.

Compare the performance of GAT and GCN for \(10\) random runs on this task and use hyperparameter search on the validation set to find the best model.

Model	F1 Score(micro)
GAT	\(0.975 \pm 0.006\)
GCN	\(0.509 \pm 0.025\)
Paper	\(0.973 \pm 0.002\)

The table above is the result of this experiment, where you use micro F1 score to evaluate the model performance.

Note

Below is the calculation process of F1 score:

\[ \begin{align}\begin{aligned}precision=\frac{\sum_{t=1}^{n}TP_{t}}{\sum_{t=1}^{n}(TP_{t} +FP_{t})}\\recall=\frac{\sum_{t=1}^{n}TP_{t}}{\sum_{t=1}^{n}(TP_{t} +FN_{t})}\\F1_{micro}=2\frac{precision*recall}{precision+recall}\end{aligned}\end{align} \]

• \(TP_{t}\) represents for number of nodes that both have and are predicted to have label \(t\)

• \(FP_{t}\) represents for number of nodes that do not have but are predicted to have label \(t\)

• \(FN_{t}\) represents for number of output classes labeled as \(t\) but predicted as others.

• \(n\) is the number of labels, i.e. \(121\) in our case.

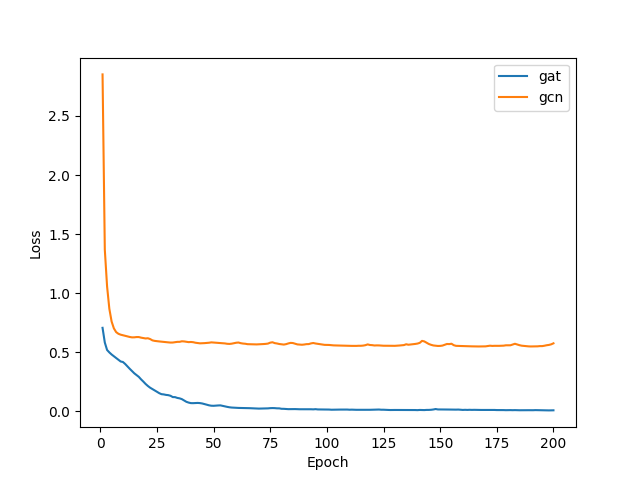
During training, use BCEWithLogitsLoss as the loss function. The learning curves of GAT and GCN are presented below; what is evident is the dramatic performance adavantage of GAT over GCN.

As before, you can have a statistical understanding of the attentions learned by showing the histogram plot for the node-wise attention entropy. Below are the attention histograms learned by different attention layers.

Attention learned in layer 1:

Attention learned in layer 2:

Attention learned in final layer:

Again, comparing with uniform distribution:

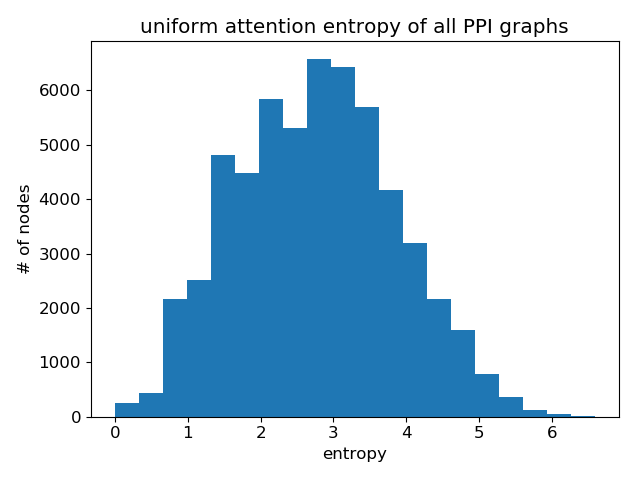
Clearly, GAT does learn sharp attention weights! There is a clear pattern over the layers as well: the attention gets sharper with a higher layer.

Unlike the Cora dataset where GAT’s gain is minimal at best, for PPI there is a significant performance gap between GAT and other GNN variants compared in the GAT paper (at least 20 percent), and the attention distributions between the two clearly differ. While this deserves further research, one immediate conclusion is that GAT’s advantage lies perhaps more in its ability to handle a graph with more complex neighborhood structure.

What’s next?

So far, you have seen how to use DGL to implement GAT. There are some missing details such as dropout, skip connections, and hyper-parameter tuning, which are practices that do not involve DGL-related concepts. For more information check out the full example.

• See the optimized full example.

• The next tutorial describes how to speedup GAT models by parallelizing multiple attention heads and SPMV optimization.